One approach to derive the functional form of money demand is that based on inventory control theory common in many models of operations management. In this approach, optimal cash balances are based on minimizing the total cost of holding these cash balances. This total cost is based on the sum of making transactions into or out of cash and the increasing opportunity cost of holding larger balances.

This cost relationship can be expressed as follows:

min C = b(Y/M) + M(i)

where:

• b = the cost of making a single cash transaction (i.e., withdrawals from a checking or savings account or conversion into stocks and bonds).
• Y = Income.
• i = a market-determined interest rate or yield.
• M = the size of Cash Balances.

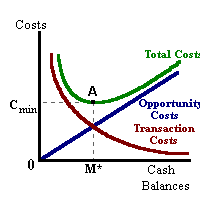
The ratio Y/M represents the number of transactions made per time period. For example is an individual's income is $2,000 per month and he/she holds on average $400 at any point in time, that individual will make 5 transactions per month. A smaller amount held as cash balances results in a greater number of transactions being made per time period and thus an increase in the cost of holding these cash balances. Given this second component, larger cash balances result in greater opportunity costs measured in foregone interest income. Thus a tradeoff exists where an individual may want to hold larger cash balances to minimize the transactions costs but may want to hold smaller balances to reduce the opportunity cost of holding these balances. These cost relationships may be seen in the following diagram:

Cost of Holding Cash Balances

Minimizing the sum of these costs implies finding the lowest point on the total cost curve in the above diagram. This point occurs at point 'A' corresponding with optimal balances of 'M*' This optimal value may also be found by using calculus and taking the derivative of the cost function with respect to M and setting the result equal to zero:

dC/dM = -bY/M² + i = 0

or

bY/M² = i

or

M* = (bY/i)^1/2 = (bY)^1/2(i)^-1/2

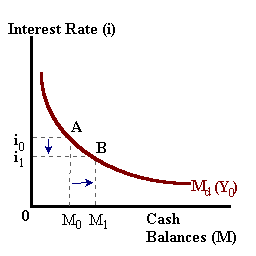
also known as the "square-root" rule. The above result states that optimal cash balances M* are directly related to income 'Y' and inversely related to interest rates 'i.

In more general form, a money demand equation with similar functional form could be written as:

M_d* = A(Y)^ρ(i)^β

such that 'ρ' greaterthan 0 and 'β' lessthan 0 such that these two exponents respectively represent the income elasticity and interest-rate elasticity (sensitivity) of money demand. The leading coefficient 'A' captures the effects of changing transactions costs and financial innovation over time.

An increase in income Y = NGDP will have the same effect by shifting the Money Demand function outward.

Money Demand	Income changes.

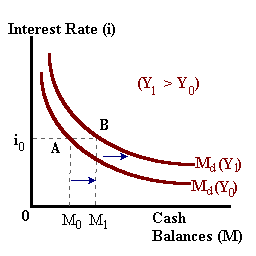These shifts in money demand and their causes will be important in the study of interest rate determination and monetary policy responses.