
The portfolio model is based on the notion that individuals hold diversified portfolios containing both cash and securities or other financial assets. The goal of these individuals is to maximize the expected return 'E[R]' of a particular portfolio while trying at the same time to minimize the financial risk 'r0' associated with that portfolio. This optimization problem can be stated as follows:
max U = f(E[Return], risk)s.t.
Market determined risk-return combinations.
Unique to the objective function is that it contains an economic good (Expected Return) and an economic bad (financial risk) or:
dU/dR > 0 and dU/dr < 0
Expected return in this model is the total dollar return from the portfolio (interest, coupon or dividend payments) and risk is based on the variability of these returns in a given portfolio. Risky portfolios may pay higher returns but there is an equal probability of large losses. Less risky portfolios involve lower returns but also smaller losses. Utility maximizing investors seek to maximize return and minimize the risk associated with any portfolio subject to the risk-return combinations defined by financial markets.
Indifference curves represent the wealth-holder's preferences for expected return on a portfolio and the risk associated with that portfolio.

A given point on an indifference curve represents a combination of risk and return that yields the same level of utility as any other point on that curve. Indifference curves that are to the northwest of any other curve represent higher levels of utility. A portfolio with a greater level of risk for the same return (i.e., moving in the eastern direction) makes this individual worse off. Portfolios with higher returns for similar levels of risk (i.e., moving in the northern direction) makes this individual better off.
One method to minimize risk is for an investor to hold all of his/her wealth in cash. Given this approach there is a zero probability of a loss (with the exception of inflation risk). However, holding all cash also means a zero rate of return. Holding the entire portfolio in securities may maximize the return but perhaps at an unacceptable level of risk. These indifference curves represents individual preferences that will allow for the determination of an optimal combination of cash and securities given an investor's preferences for risk and return (some individuals might be risk-seeking, other individuals are risk-averse).
Risk is often measured by taking a historical look at the variability of the return in an asset over time. This variability may be computed using a variance or some other measure of variation:
σ2 = (1/n) Σ(Rt - E[R])2
The larger the variance for a particular asset the greater the risk. As an extension, when making a comparison among different assets this variance measure must be scaled to adjust for the magnitude of the dollar-value of the returns being considered. This scaling is accomplished simply by dividing the measure of variation by the mean (average) of the returns:
σ2 / E[R]
The optimum is found where a given indifference curve is just tangent to a market-determined risk-return locus.. This locus represents actual combinations of risk and return as determined by primary and secondary financial markets.
In the diagram below, risk is measured in the horizontal axis and expected return 'E[Return]' is measured on the vertical axis. The indifference curves IC0, IC1, IC2, are upward sloping representing the fact that return is desired by the investor and risk is normally avoided by the investor. The point where an indifference curve intersects the vertical axis represents the level of risk for risk-free assets such as government securities.
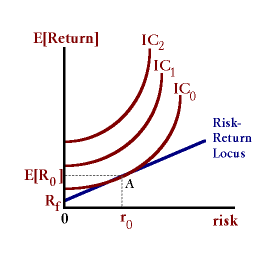
The straight line is the risk-return locus. The vertical intercept of this line represents the actual return 'Rf 'on a risk-free asset such as the return on T-bills. The slope of this line represents market-determined combinations of portfolio risk and corresponding returns. If market interest rates (yields) increase, then a given portfolio containing some proportion of securities will deliver a higher return for the same level of risk. The slope of this risk-return locus will rotate upwards.
Any point of tangency between an indifference curve and the risk-return represents an optimum -- a point where the preferences of the investor match exactly with the reality of the market.
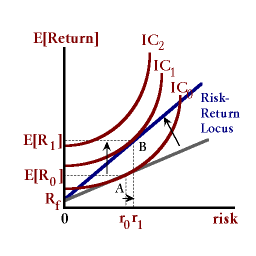
As market rates increase from i1 to i2, the investor optimum moves from point 'A' to point 'B', i.e., the investor is willing to assume more risk (by holding more bonds in the portfolio) r1 to r2 given the higher yields available in the market. An increase in market rates will induce investors (wealth-holders) to hold a greater proportion of financial securities in their portfolios and less cash. The greater returns 'R' available for only a little more risk will make these investors better off.
This portfolio model provides another look at how changes in interest rates affect money demand -- cash balances being one element of diversified portfolio of assets. Higher interest rates can induce the owner of this portfolio to absorb more risk by holding more of these riskier assets and less cash.
|
|