A bond represent a long-term debt contract between a borrower and lender. The terms of this contract include the face value (the amount borrowed per bond issued) F, a rate of (annual or semi-annual) interest r, and the maturity (the date when the face amount must be repaid) N. The coupon of the bond R represents the periodic dollar amount of interest paid to the lender/owner of the bond over the life of that bond. This coupon amount is calculated simply by taking the product of the face value and rate of interest:
R = (F) x (r)
The price (or present value) a bond with coupon 'R' and a face value of 'F' at the end of 30 years is defined by the following formula:
Pbond = PVbond = Σ[t=1,30] Rt(1+r)-t + F(1+r)-30
or using the formula for the sum of a geometric series:
= (R/r)[1 - (1+r)-30] + F(1+r)-30
If the rate of discount 'r' is the same as the printed interest rate on the bond (so that R/r = F) then the above expression reduced to:
Pbond = F
As 'N' approaches infinity, (the Bond never matures) for any rate of discount this expression reduces to:
Pbond= (R/r)
which is known as the present value of a perpetuity and provides a simple formula for understanding the relationship between asset prices 'P' and asset yields 'Ψ' (or interest rates).
Ψ = R / Pbonds
The coupon payment and face value are fixed by contract over the life of the bond. If market interest rates are the same as the printed rate of interest on the bond, then the price (present value) of that bond is the same as its face value-- the bond sells at par-value. If market interest rates have risen, prior to the sale of the bond, such that investors can receive higher yields on competing investments; then, the market price of the bond will be less than its face value. The bond will sell at a discount. If the opposite is true such that market rates have fallen, then the bond will sell at a premium -- the market price will exceed its face value. Bond prices move in the opposite direction of market interest rates.
You can practice with the model below:
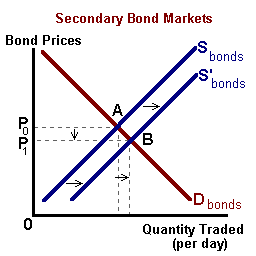
Activity in secondary markets often reflects changes in the economic environment where buying and selling activity is driven by changes in inflationary expectations, changing attitudes towards (credit and interest rate) risk, and changes in perceived uncertainty about the future.

For example, suppose that information becomes available such that investors revise their inflationary expectations upward. Given that inflation lowers the real rate of return received by lenders (or those holding bonds and other securities), these individuals will begin to sell existing bonds in the secondary market. This selling creates a surplus of bonds being offered such that bond prices must fall to induce potential buyers to accept these securities in an accelerating inflationary environment. With this decline in bond prices, secondary bond yields increase:
R / Pbonds ↓ = Ψ ↑
When yields rise, investors have the option of buying existing bonds in the secondary bond market or new bonds in the primary market. In order for these new bonds to be competitive with existing bonds, a higher rate of interest must be offered. This higher rate of (nominal) interest will reflect the upward revision of expected inflation.
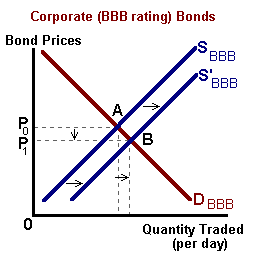
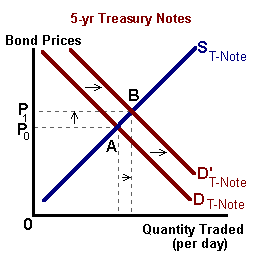
Secondary markets also facilitate portfolio adjustments in reaction to a changing economic environment or changes in individual preferences for risk. For example given two different assets one being higher risk (a BBB rated 5 year corporate bond) and the other no risk (i.e., a Treasury Note), we would expect that:
ΨCorporate-BBB > ΨT-Note such that ρ = (ΨCorp.-BBB - ΨT-Note)
If for some reason the perceived risk of holding debt instruments were to increase, we would expect to observe a flight to quality – a selling the corporate bonds and buying of Treasury instruments.
|
|
Increased selling will drive the price of Corporate bonds down and buying activity will drive the price of Treasury Notes up or:
PCorporate-BBB ↓, ΨCorporate-BBB ↑ and PT-note↑, ΨT-note↓
such that
ΨCorporate-BBB - (ΨT-note) ↑ -- ρ ↑
Common stock represent ownership (equity) shares in publicly-held corporations. These rights of ownership often include a share in the profits (earnings) of that corporation. However, these earnings may be used either as a source of internal financing , known as retained earnings, or paid out to the owners as dividends. The value of the corporation is based on these earnings 'Et whether they are paid out or not.
Pshare = ΣEt/(1 + r)
Much is made of the price/earnings (PE) ratio of different common stocks with a low PE being often preferred to a high PE for a given stock. This ratio is often used as a benchmark to determine if that corporation is overvalued (too high) or undervalued(too low)by the stock market based on its current trading price. This ratio is nothing more than the reciprocal of a simple yield calculation based on the present-value of a perpetuity formula:
Passet = (R/r)
or
Ψasset = R/Passet
or
Ψstock = Earnings/Pshare
The earnings-over-price ratio is often in percentage form and by taking the reciprocal we define an integer expression that is often easier for use in making comparisons among different stocks. However, for purposes of evaluation, we can use the reciprocal of the PE and compare with investments of equivalent risk and maturity or against the yields on perhaps safer marketable assets.
What is unique about equity instruments is that their value often is based not just on the periodic return (earnings in this case) but also the expected rate of growth for the corresponding corporation. The rate of return on common stock is often (usually for well-established mature corporations) calculated by the following formula:
Ψ = E/Pshare + E[g]
where 'Ψ' is the rate of return, 'E' represents annual earnings (or dividend), 'P' is the purchase price of a share of the stock, and E[g] is the expected growth rate in future dividends.
Given an annual dividend of $1.00, a purchase price of $30.00 per share, and an expected growth rate of 5%; the rate of return would be:
Ψ = ($1.00/$30.00) + .05 = .0333 + .05 = 8.33%
This formula can also be used to determine the appropriate price to be paid per share of stock given expected growth rates in the annual dividend and some measure of the rate of return 'r*' based on similar investments. Solving for 'P', we have:
Pshare = E/(r* - g)
or given annual earnings of per share of $2.00, an expected (or required) rate of return of 8%, and an expected growth rate in future dividends for that company of 3% per year; we can calculate purchase price as:
P = $2.00 / (0.08 -0.03) = $40.00
Quite often the explanation for the existence of both buyers and sellers of the same shares of stock is that buyers expect higher growth rates in future dividends relative to the expectations of sellers.
Most Treasury bills and/or commercial paper (due to their short maturity -- 1 year or less) are discounted at the time of sale rather than pay some coupon payment over the holding period. This discount is calculated as follows:
Discount = (F) x (r) x [(d)/ 365]
where F is the face value (the amount borrowed or principal), 'd' is the days to maturity, and r is the market interest rate.
For example, if a business needs to borrow roughly $1,000,000 for six months (182 days) to finance seasonal inventory needs, and current market rates are 10% then the amount of the discount would be:
($1,000,000) x (0.10) x (182/365) = $49,683
thus the actual amount borrowed by that business firm is:
$1,000,000 - $49,683 = $950,137
However the full $1,000,000 is repaid at the maturity date.
The rate of return (the yield) on this short-term debt instrument is equal to the amount of the discount divided by the amount borrowed or:
$49,683 / $950,137 = Ψ = 5.23% semiannually
or an effective rate of: (1.0523)2 - 1 = 10.7% annually
Trading of money market instruments of particular face value ‘F’ is based on prices offered for these instruments in secondary markets or via auction in primary markets. The yield is then computed as follows:
Ψdiscount = (F - Poffered)/Poffered = (F / Poffered) - 1such that as,
Poffered ↑, Ψdiscount ↓
Since both stocks and bonds are marketable securities, the potential exists for changes in market price which may translate into capital gains or perhaps capital losses. A capital gain occurs when the selling price of a security 'Ps' exceeds the purchase price 'Pp'. If the selling price is less than the purchase price then the owner will incur a capital loss.
Capital gains and losses can either enhance or reduce the normal rate of return on a given security. For this reason, acquisition of these securities are often based on expectations of future capital gains in addition to the normal rate of return. This overall yield or expected total rate of return 'E[TRR]' defined as follows:
E[TRR] = rn + (E[Ps]- Pp)/Pp
where 'rn' represents the normal rate of return ( current yield -- R / Pp) on the security and 'E[Ps]' represents the expected selling price of the security at some point in the future.
Expectations about the selling price (E[Ps]) depend on expected changes in market interest rates (such that these prices and interest rates will move in opposite directions), and/or expected rates of growth in earnings (in the case of equities). Lower market interest rates or higher rates of growth can lead to capital gains on the sale of these assets such that the ETRR is greater than the current yield.
If market interest rates are expected to increase or growth rates in earnings are revised downwards, then these asset may sell a price below the price paid and thus a capital loss results. In this case the ETRR may be less than the current yield and, in the case of an extreme increase in interest rates, be negative if with a significant decline in the selling price (the capital oss more than offsets the normal yield).
In situations where investors expect the total rate of return to be negative on a financial asset, cash will present a suitable alternative given that:
TRRcash = 0
Thus solid reasons may exist for holding cash in a portfolio of financial assets even though cash does not pay any type of periodic return. In the expectation of capital losses on marketable securities, principal may be preserved by holding cash.
|
|