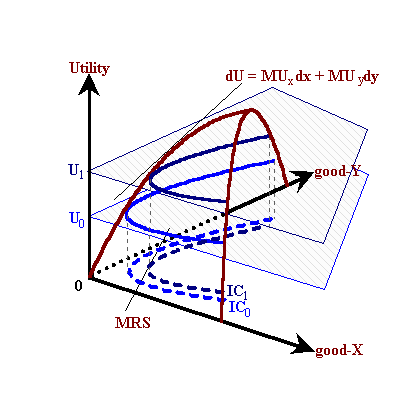
Given a utility function: U = f(x,y), we can diagram this as a utility surface with the two goods measured along the base and utility measured as the height as shown in figure 1:

figure 1 -- the Utility Surface

This utility surface is a concave function based on our assumptions of diminishing marginal utility. Changes in elevation represent increasing levels of utility. Traversing the surface such that we hold elevation constant help to identify one particular indifference curve as a convex set in the x-y plane.

Using this utility function, we calculate separate expressions for the marginal utility of good-x and good-y:

dU/dx = MU_x -- holding 'y' constant

or dU_x = MU_xdx -- the equivalent of climbing the hill by traveling due east (along the 'x' axis).

dU/dy = MU_y -- holding 'x' constant

or dU_y = MU_ydy -- the equivalent of climbing the hill by traveling due north (along the 'y' axis).

These marginal utilities represent a measure of the slope or steepness of the hill as we traverse in the due-east or due-north directions. With respect to the notion of utility, we can think of these marginal utilities as the rate by which consumption of either good is transmitted (or converted) into additional into utility or satisfaction.

Combining these separate transmission mechanisms, we can identify how utility changes with consumption of one or both goods:

dU_total = dU_x + dU_y

= MU_xdx + MU_ydy -- climbing the hill by moving in the north-east direction.

Holding utility constant (dU_total = 0) or traversing the surface allows us to write:

0 = MU_xdx + MU_ydy

or

dy/dx = -MU_x/MU_y

Thus, the slope of an indifference curve at a given point in the x-y plane represents a measure of the ratio of marginal utilities which is also known as the marginal rate of substitution (MRS). This represents the rate at which one good must be substituted for another in order to keep the level of utility constant.