
Production in the long run is distinguished from short run production in that all factor inputs may be used in varying amounts. Given the production function:
X = f(L, K, M, R),
we find that one factor may be substituted, to some degree, for another factor of production. Increasing the amount of capital or machinery 'K' can replace some labor 'L' but not all of the labor in a production process. Increasing amounts of labor (greater care being taken in production to avoid waste) can reduce the need for some material inputs 'M'. In addition, where all factors of production are allowed to vary in quantity, proportional increases in all factors of production may lead to unbounded increases in output.
As we begin to model production in the long run, we will simplify the production function somewhat as:
X = f(L, K),
where we assume that the extraction of raw materials or the development of land is accomplished with combinations of labor and capital input. Entrepreneurship is embedded in the production technology used [f(.)]. This allows for a two-dimensional representation of combinations of factor inputs required to produce chosen levels of output.

Suppose, for example, it is possible to produce 100 units of output (X = 100) with the following combinations of labor and capital :
| L | K | |
| 50 | 200 | -- Capital Intensive Production |
| 100 | 100 | -- Equal Amounts |
| 200 | 50 | -- Labor Intensive Production |
Each point represents these input combinations. The lines connecting each point denote the possibility that an arithmetic average of any of these combinations may also allow for the production of 100 units of output.
If the production technology allows, we could double the quantity of each input and perhaps double the amount of output . These points represent capital and labor combinations that allow for this greater level of output. By tripling the original quantity of intputs might allow for a tripling of output .
The 'kinked' lines in the above diagram are known as Production Isoquants or "lines of equal output". Each point on a given colored line represents combinations of the two inputs that allow for a given level of output: X = 100, X = 200, or X = 300.
Points A, A', or A'' represent combinations of capital and labor used in a 4:1 ratio in order to produce the three levels of output. In relative terms, this is known as Capital Intensive Production (press the 'K/L Ratio' button in the diagram above).
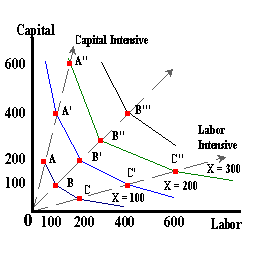
The points C, C', or C'' represent combinations of capital and labor used in a 1:4 ratio or Labor Intensive Production. For a given production technology it is not possible to say that using one factor more intensively than the other is better or more efficient. In economies where capital is relatively scarce and therefore relative more expensive in use as compared to labor, a labor intensive production process may be more efficient. If the opposite is true (labor being relatively scarce), then capital intensive production may be observed. The actual combination of factor inputs will depend on their relative prodcutivities and existing factor prices.
The three rays representing different production processes (capital intensive, labor intensive, or in-between), may not be the only options available. Allowing for a continuim of processes results in the 'kinked' production isoquants becomming smoother. These smooth isoquants represent an infinite number of production processes available.
Through an examination of proportional increases in the inputs, we can define different production technologies with the concept of returns to scale. This concept refers of the ability to more than double, exactly double, or less than double the level of output when the quantity of all the available inputs are exactly doubled.
For example, in some cases, a production process may be replicated. Thus if a certain quantiy of grain is being produced on one acre of land with 5 units of labor input and 3 pieces of capital, then by replicating this production process the quantity of grain produced may be doubled. In this case, the technology represented is known as constant returns to scale.

Technologies where a doubling of inputs leads to a more than doubling of outputs is known as increasing returns to scale. Finally production techologies that lead to a less than doubling of output when all inputs are doubled is known as decreasing returns to scale.
Figure 4, Increasing Returns to Scale
|
Figure 5, Decreasing Returns to Scale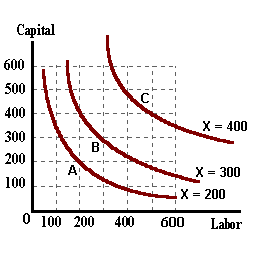 |
One mathematical production relationship that posesses the three properties listed above (diminishing marginal productivity, essential inputs, and possibilities for substitution) is the Cobb-Douglas production function. This particular representation is one of several possibilities and may be written as follows:
X = AtLαKβ
where L and K represent the factor inputs listed above, A represents a measure of technology at time period 't', and the exponents represent production parameters (actually output elasticities). The fact that it is multiplicative in the inputs reflects the notion that one factor may be substituted for another. Diminishing marginal productivity requires that the exponents 'α' and 'β', each take on values less than one.Each input being essential and making a positive contribution to output implies that these exponents be strictly greater than zero.
The different production technologies are defined by the sum of the production exponents. Constant returns to scale implies that α and β, sum to one:
Note:
X = At Lα Kβ
and
At(2L)α (2K)β =
(2)α + β At Lα Kβ =
(2)1 At Lα Kβ = 2X
With increasing returns to scale these exponents will sum to a value greater than one and with decreasing returns to scale, these exponents sum to a value less than one.
Returns to scale represent one dimension of production technology in the long run. This concept governs how costs change as production levels are altered. Under constant returns to scale, a doubling of output results in an exact doubling of production costs. In the case of increasing returns, costs increase at a rate less than than change in output such that average (per-unit) costs decrease with increasing levels of output. On the other hand, under decreasing returns to scale, costs increase at a rate greater than production. In this case, increasing production levels are matched by increasing per-unit costs.
A second dimension to production technology is the ease by which one factor may be substituted for another. This may be necessary as relative factor prices change (i.e., wages increase such that labor becomes more expensive relative to capital) and the firm attempts to substitute away from the more expensive factor.
The Cobb-Douglas production function is just one particular mathematical form consistent with imperfect substitution among factors.
Two extreme cases are a Linear Technology where the production function may be written as:
X = αL + βK
In this case, the factors are perfect substitutes for one another and the profit maximizing firm will use only the relatively cheaper factor of production.
At the other extreme is a Leontief Technology where factors must be used in fixed proportion to one-another (i.e., in providing passenger services, one bus is matched with one driver):
X = min[αL, βK]
In this case, substitution is not possible and the firm must absorb factor price increases in the form of higher costs.
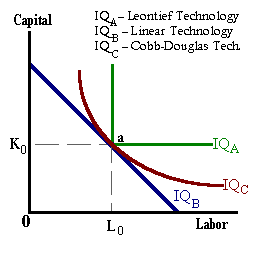
These different expressions may be summarized in a single mathematical form known as the Constant Elasticity of Substitution (CES) production function:
X = A[αLρ + βKρ](1/ρ)
The new paramter introduced 'ρ' is a measure of the ease by which labor may be substituted for capital or vice-versa. If the following values of ρ are observed:
ρ = 0 -- then we have a Cobb-Douglas technology,
ρ = 1 -- then we have a Linear technology,
as ρ approaches negative infinity -- then then a Leontief technology exists.
|
|