The creation of Physical and Human Capital represents production not intended for direct consumption. Rather, the creation and accumulation of capital is intended to increase the level of productivity of a nation and thus allow for an increase in the production of goods and services at future date.

Capital may be thought of as an Intermediate Good or a good used to produce other goods.

The creation and accumulation of capital depends on the ability of a nation to give up current consumption of Final Goods (goods used for direct consumption) to make resources available for the accumulation of this capital. Deferring consumption (known as savings) depends on the ability of that nation to first meet the basic needs of its citizens with existing production technology and resource availability. A country that exists on the frontier of subsistence could make resources available for the creation of capital only at the expense of feeding a given proportion of its population. In this case, capital accumulation comes with the price of starvation.

3.3.1 The Solow Growth Model

One way to understand the relationship between current production, savings activity and the accumulation of capital is via the Solow Growth model. defines the conditions for the tendency of different nations to approach an equilibrium (steady-state) level of the capital stock.

We begin by using an economy-wide production function in Cobb-Douglas form with constant returns to scale:

Y* = f(L,K) = AL^αK^{1 - α}

As a first step, we modify this expression to put it into a form that represents the standard of living (simply the ratio of output to labor input):

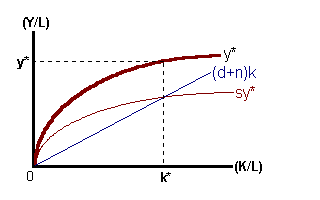
y* = Y*/L = f(1,K/L) = A(K/L)^{1 - α} = Ak^{1 - α}

The term 'k' represents the capital/labor ratio better understood as the amount of capital available per unit of labor input. We would expect that greater amounts of capital per labor-unit would make that labor more productive and thus raise the living standards within a particular nation.

Capital is unique in that over time it wears out. This factor input is subject to the effects of friction, obsolescence and climate such that at some future date it ceases to make a useful contribution to the production process. This is known as depreciation. The reciprocal of the life-span of a unit of capital is then defined as the rate of depreciation 'δ'. The implication of this is that without replacement (via investment expenditure) the capital-labor ratio would naturally decline over time. In order to maintain this ratio, the required level of investment 'I_required' (a flow variable) must be equal to the depreciation in the capital stock:

I_required = δ K

It must be noted that with greater amounts of capital in place, greater levels of investment are required to maintain a particular capital-labor ratio (i.e., the more capital that exists, the more capital there is to wear out in a given time period).

With growth in the size of the labor force (due to population growth and increasing labor-force participation rates), additional investment is also necessary to maintain the capital-labor ratio (K/L) at a particular level. Thus, the level of investment must exceed rate of depreciation by an amount equal to the growth-rate 'n' in the labor-force:

I_required = (n + δ)K

or if we divide both sides by 'L'

i _required = (n + δ)k

Investment is possible only if a given country makes resources available for this accumulation of capital. These resources, known as savings, represent those goods produced in the current time period not devoted to final private or public consumption. In a closed economy, we could write the following:

Savings: S = Y* - C - G S = sY*

where 's' represents the marginal propensity to save or the proportion of output not devoted to private consumption 'C' or public (Government) consumption 'G'. With efficient financial and capital markets, these savings could then be made available for investment in new capital:

Savings = I_required

sy* = (n + δ)k

The Solow Growth Model -- Steady State

If sy* < (n + δ)k then δ k < 0, then savings (and thus investment) is below the level necessary to compensate for the rate of depreciation and growth in population and thus, the capital-labor ratio is decreasing. If the opposite is true then δ k > 0, and the amount of capital available per unit of labor is increasing. This latter situation leads to economic growth as measured by changes in per-capita output

According to this model, an increase in the rate of savings leads to growth in the capital stock and therefore a higher Standard of Living. Reductions in population growth rates 'n' may accomplish the same result.

An increase in the savings rate.

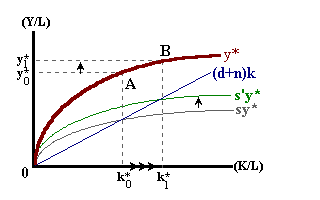
It is important to note that even though an economy may be in a "steady-state" condition, this does not imply that there is no growth in factor inputs or output. If k is constant, this implies that the %Δ K = %Δ L. In addition, given that y* is also constant in the steady state, %Δ Y* = %Δ L. Thus we can write:

%Δ Y* = %Δ L = %Δ K

or

%Δ Y* = α [%Δ L] + (1 - α)[%Δ K]

If we observe an economy with a growth rate that exceeds the rate of population growth, we can conclude that this economy is currently below its steady state level of capital per unit or labor or to exogenous changes in technology (i.e., the %Δ A_t > 0).